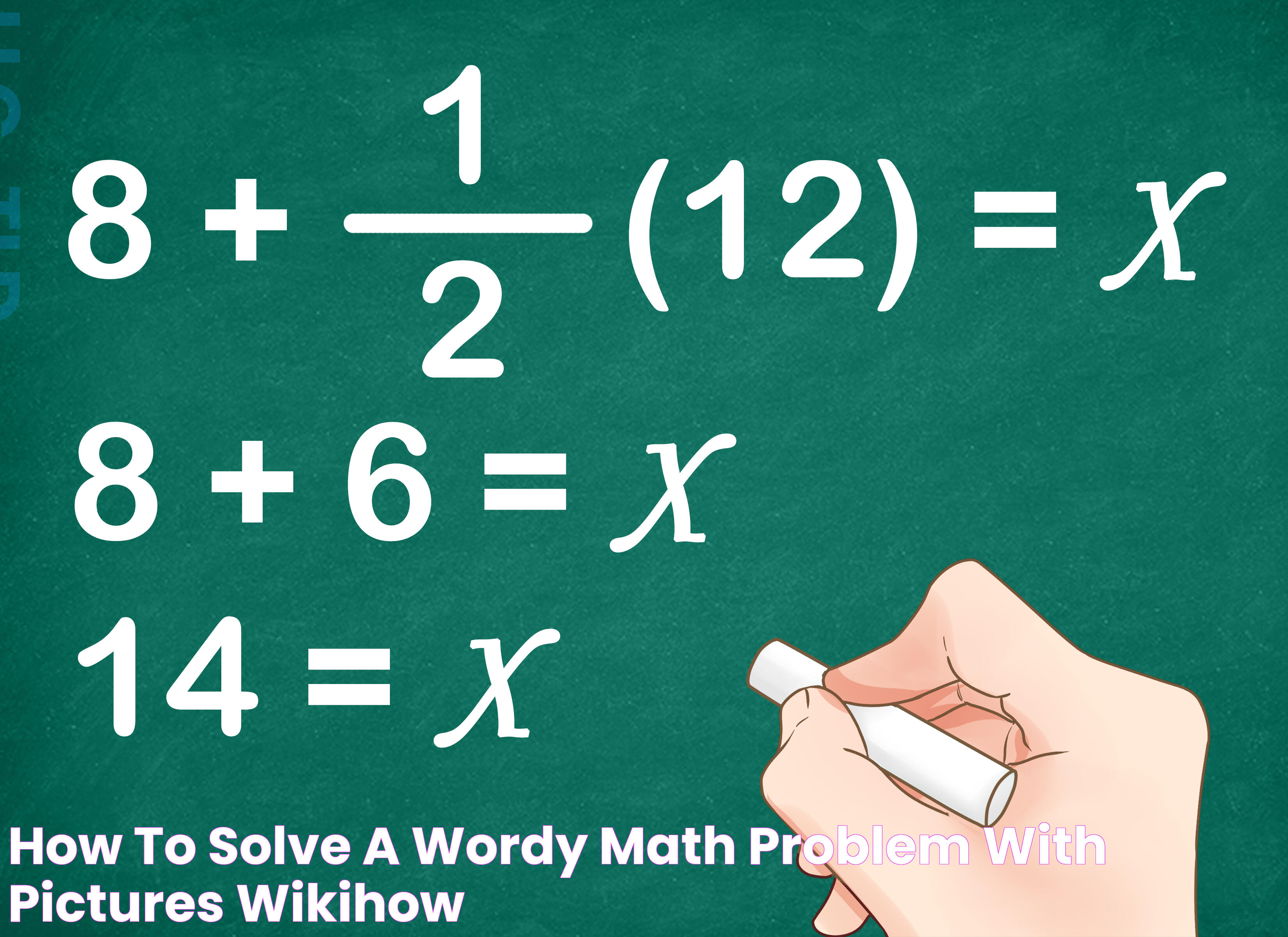Math problems can often feel like daunting challenges, but they also offer an opportunity to develop critical thinking and problem-solving skills. Whether you're solving equations or tackling geometry, mastering math problems is an essential part of education that extends beyond the classroom. Understanding the nuances and techniques for solving various math problems can help you excel academically and gain confidence in your mathematical abilities.
At its core, solving math problems is about understanding concepts and applying logical reasoning. With the right strategies, anyone can learn to break down complex math problems into manageable steps. This not only makes math more approachable but also enhances your ability to analyze and solve problems in other areas of life. Furthermore, math problems can be a fun and rewarding way to challenge your mind and improve your cognitive skills.
This comprehensive guide will delve into the world of math problems, covering a variety of topics to help you become proficient in solving them. From understanding basic arithmetic to tackling advanced calculus problems, we'll explore the essential techniques and strategies for success. Whether you're a student, educator, or lifelong learner, this article aims to provide valuable insights and practical advice for solving math problems with ease and confidence.
Read also:Enhancing Your Look With Burgundy Wine Hair A Complete Guide
Table of Contents
- Biography of Math Problems
- Understanding Basic Arithmetic
- Dive into Algebra: Formulas and Equations
- Geometry Explored: Shapes and Theorems
- Calculus Concepts: Derivatives and Integrals
- Math Problems in Real Life: Practical Applications
- Problem-Solving Strategies: Tips and Techniques
- How to Overcome Math Anxiety?
- Math Problems and Technology: Tools and Resources
- Why is Practice Important in Math?
- Math Competitions: Challenges and Benefits
- Fostering a Love for Math in Students
- Common Misconceptions About Math Problems
- Math Problems in History: Significant Milestones
- Frequently Asked Questions
- Conclusion: Embracing Math Problems
Biography of Math Problems
Math problems have been an integral part of human history, influencing various aspects of society, science, and technology. From ancient times to the modern era, math problems have evolved, reflecting changes in human understanding and technological advancements. The study of math problems is not just about numbers and formulas; it's about exploring patterns, structures, and relationships that define the world around us.
Historically, math problems were often practical in nature, developed to address real-world challenges such as trade, construction, and astronomy. Over time, mathematicians began to formalize these problems, creating abstract concepts and theories that laid the foundation for modern mathematics. Today, math problems encompass a wide range of topics, from simple arithmetic to complex calculus, each with its own unique set of challenges and applications.
As math problems have become more sophisticated, so too have the methods for solving them. Advances in technology, particularly in computing, have revolutionized the way we approach math problems, allowing for more efficient and accurate solutions. Despite these changes, the fundamental principles of problem-solving remain the same: understanding the problem, developing a strategy, and executing the solution with precision and creativity.
Understanding Basic Arithmetic
Basic arithmetic forms the foundation of all math problems, encompassing the four fundamental operations: addition, subtraction, multiplication, and division. These operations are the building blocks of mathematics, used in a wide variety of contexts from everyday calculations to complex problem-solving scenarios.
Understanding basic arithmetic involves not only knowing how to perform these operations but also recognizing their properties and relationships. For example, the commutative property of addition and multiplication states that the order of numbers does not affect the result, while the associative property allows for grouping numbers in different ways to simplify calculations. Mastery of these concepts is essential for tackling more advanced math problems.
In addition to operations, basic arithmetic also includes understanding numbers and their properties. This includes recognizing different types of numbers, such as integers, fractions, and decimals, as well as concepts like place value and rounding. By developing a strong foundation in basic arithmetic, you can approach more complex math problems with confidence and ease.
Read also:Discover The Impact Of Ozempic Face A Comprehensive Analysis
Dive into Algebra: Formulas and Equations
Algebra represents a significant leap from basic arithmetic, introducing variables, formulas, and equations into math problems. In algebra, numbers are often represented by letters, allowing for the expression of general relationships and patterns. This abstraction is a powerful tool for solving a wide range of math problems, from simple equations to complex systems.
One of the key concepts in algebra is the equation, a mathematical statement that asserts the equality of two expressions. Solving equations involves finding the value of the variable that makes the equation true. This process often requires the use of algebraic techniques such as factoring, substitution, and the application of the distributive property.
Algebra also introduces the concept of functions, which describe a relationship between two sets of numbers. Understanding functions and their properties is essential for solving more advanced math problems, particularly those involving calculus and higher-level mathematics. By mastering the basics of algebra, you can develop the skills necessary to tackle a wide range of math problems with confidence and creativity.
Geometry Explored: Shapes and Theorems
Geometry is the study of shapes, sizes, and the properties of space. It is a branch of mathematics that deals with the properties and relationships of points, lines, surfaces, and solids. Geometry problems often involve the application of theorems and formulas to calculate measurements and prove relationships between geometric figures.
One of the most well-known theorems in geometry is the Pythagorean theorem, which relates the sides of a right triangle. This theorem is a fundamental tool for solving a variety of geometry problems, from determining distances to calculating areas and volumes. Other important concepts in geometry include congruence, similarity, and symmetry, each of which plays a crucial role in solving geometry problems.
In addition to these concepts, geometry also involves the study of transformations, such as translations, rotations, and reflections. Understanding these transformations is essential for solving problems involving coordinate geometry, a branch of geometry that uses algebraic techniques to study geometric figures. By mastering the principles of geometry, you can develop the skills necessary to solve a wide range of math problems with precision and accuracy.
Calculus Concepts: Derivatives and Integrals
Calculus is a branch of mathematics that deals with change and motion. It is a powerful tool for solving a wide range of math problems, from analyzing the motion of objects to modeling complex systems. Calculus involves two main concepts: derivatives and integrals, each of which plays a crucial role in solving calculus problems.
The derivative is a measure of how a function changes as its input changes. It is a fundamental tool for analyzing rates of change and is often used in physics and engineering to model dynamic systems. The integral, on the other hand, is a measure of the accumulation of quantities, such as area under a curve or the total distance traveled by an object.
Understanding these concepts requires a solid foundation in algebra and geometry, as well as the ability to think abstractly and logically. By mastering the principles of calculus, you can develop the skills necessary to solve a wide range of math problems, from simple rate problems to complex optimization problems.
Math Problems in Real Life: Practical Applications
Math problems are not just abstract concepts; they have practical applications in a wide range of fields, from science and engineering to finance and medicine. Understanding how to solve math problems can help you make informed decisions, analyze data, and solve real-world challenges.
In science, math problems are used to model natural phenomena, such as the motion of planets or the behavior of cells. In engineering, math problems are used to design and analyze structures, from bridges to skyscrapers. In finance, math problems are used to calculate interest rates, evaluate investments, and manage risk.
By understanding the practical applications of math problems, you can develop the skills necessary to solve real-world challenges and make informed decisions in your personal and professional life.
Problem-Solving Strategies: Tips and Techniques
Solving math problems requires more than just knowledge of formulas and equations; it requires a strategic approach to problem-solving. By developing effective problem-solving strategies, you can approach math problems with confidence and creativity.
One effective problem-solving strategy is to break the problem down into smaller, more manageable parts. This can help you identify the key elements of the problem and develop a step-by-step plan for solving it. Another effective strategy is to use visualization techniques, such as drawing diagrams or creating models, to better understand the problem and its components.
Other effective problem-solving strategies include looking for patterns, using logical reasoning, and checking your work for accuracy. By developing these skills, you can approach math problems with confidence and creativity, and develop the skills necessary to solve a wide range of math problems.
How to Overcome Math Anxiety?
Math anxiety is a common problem that can affect students and adults alike. It can make math problems seem more difficult than they are and can lead to feelings of frustration and discouragement. However, with the right strategies, you can overcome math anxiety and develop a positive attitude toward math problems.
One effective strategy for overcoming math anxiety is to practice regularly. By practicing math problems on a regular basis, you can build your confidence and develop your skills. Another effective strategy is to break problems down into smaller, more manageable parts, and to focus on understanding the underlying concepts rather than just memorizing formulas.
Other effective strategies for overcoming math anxiety include seeking help from a tutor or teacher, using relaxation techniques to manage stress, and developing a positive attitude toward math. By adopting these strategies, you can overcome math anxiety and develop a positive attitude toward math problems.
Math Problems and Technology: Tools and Resources
Technology has revolutionized the way we approach math problems, providing a wide range of tools and resources to help you solve math problems with ease and accuracy. From calculators and computer software to online tutorials and educational apps, technology offers a wealth of resources for solving math problems.
One of the most powerful tools for solving math problems is the graphing calculator, which allows you to visualize mathematical relationships and solve complex equations with ease. Computer software, such as MATLAB and Mathematica, offers advanced capabilities for solving math problems, from simple calculations to complex simulations.
Online resources, such as Khan Academy and Coursera, offer tutorials and courses on a wide range of math topics, from basic arithmetic to advanced calculus. Educational apps, such as Photomath and Mathway, provide instant solutions to math problems, helping you learn and practice math skills on the go.
Why is Practice Important in Math?
Practice is essential for mastering math problems and developing the skills necessary to solve a wide range of math problems. By practicing math problems regularly, you can build your confidence, develop your skills, and improve your problem-solving abilities.
Practice allows you to reinforce your understanding of concepts and develop your ability to apply them to different types of problems. It also helps you develop your ability to think logically and creatively, and to approach math problems with confidence and creativity.
By practicing math problems regularly, you can develop the skills necessary to solve a wide range of math problems, from simple calculations to complex equations. Whether you're a student, educator, or lifelong learner, practice is essential for mastering math problems and developing your problem-solving skills.
Math Competitions: Challenges and Benefits
Math competitions offer a unique opportunity to challenge your math skills and develop your problem-solving abilities. These competitions, such as the Math Olympiad and the American Mathematics Competitions, offer a wide range of challenges, from simple calculations to complex equations.
Participating in math competitions can help you develop your problem-solving skills, build your confidence, and improve your math abilities. It can also provide a sense of accomplishment and pride, and offer opportunities for recognition and scholarships.
Math competitions offer a unique opportunity to challenge your math skills and develop your problem-solving abilities. By participating in these competitions, you can develop the skills necessary to solve a wide range of math problems and achieve success in math and beyond.
Fostering a Love for Math in Students
Fostering a love for math in students is essential for developing their problem-solving skills and encouraging a lifelong interest in mathematics. By creating a positive and engaging learning environment, educators can help students develop a love for math and a desire to tackle math problems with confidence and creativity.
One effective strategy for fostering a love for math is to make it relevant and engaging. By connecting math problems to real-world scenarios and practical applications, educators can help students see the value and importance of math in their everyday lives.
Another effective strategy is to encourage a growth mindset, emphasizing the importance of effort and perseverance in solving math problems. By encouraging students to embrace challenges and learn from mistakes, educators can help them develop a positive attitude toward math and a desire to tackle math problems with confidence and creativity.
Common Misconceptions About Math Problems
There are many common misconceptions about math problems that can make them seem more difficult than they are. By understanding and addressing these misconceptions, you can approach math problems with confidence and creativity.
One common misconception is that math problems are only for "math people." In reality, anyone can learn to solve math problems with the right strategies and practice. Another common misconception is that math problems require memorization of formulas and equations. In reality, math problems require understanding of concepts and the ability to apply them to different types of problems.
By understanding and addressing these misconceptions, you can approach math problems with confidence and creativity, and develop the skills necessary to solve a wide range of math problems.
Math Problems in History: Significant Milestones
Math problems have played a significant role in history, influencing the development of science, technology, and society. From ancient times to the modern era, math problems have been used to solve real-world challenges and drive innovation.
One significant milestone in the history of math problems is the development of calculus by Isaac Newton and Gottfried Wilhelm Leibniz in the 17th century. This powerful mathematical tool revolutionized the way we approach math problems, providing a new way to analyze change and motion.
Another significant milestone is the development of algebra by ancient mathematicians such as Al-Khwarizmi and Diophantus. This branch of mathematics introduced the concept of variables and equations, allowing for the expression of general relationships and patterns.
By understanding the history of math problems and their impact on society, you can gain a deeper appreciation for the value and importance of mathematics in our world.
Frequently Asked Questions
- What are some effective strategies for solving math problems?
Effective strategies for solving math problems include breaking the problem down into smaller parts, using visualization techniques, looking for patterns, using logical reasoning, and checking your work for accuracy.
- How can I overcome math anxiety?
You can overcome math anxiety by practicing regularly, breaking problems down into smaller parts, seeking help from a tutor or teacher, using relaxation techniques to manage stress, and developing a positive attitude toward math.
- What are some common misconceptions about math problems?
Common misconceptions about math problems include the belief that math is only for "math people" and that solving math problems requires memorization of formulas and equations. In reality, anyone can learn to solve math problems with the right strategies and practice.
- What are some practical applications of math problems?
Math problems have practical applications in a wide range of fields, including science, engineering, finance, and medicine. They are used to model natural phenomena, design and analyze structures, calculate interest rates, and manage risk.
- How can technology help with solving math problems?
Technology offers a wide range of tools and resources for solving math problems, including graphing calculators, computer software, online tutorials, and educational apps. These resources can help you solve math problems with ease and accuracy.
- Why is practice important in math?
Practice is essential for mastering math problems and developing the skills necessary to solve a wide range of math problems. It allows you to reinforce your understanding of concepts, develop your problem-solving abilities, and build your confidence in math.
Conclusion: Embracing Math Problems
Math problems offer a unique opportunity to develop critical thinking and problem-solving skills, both in the classroom and beyond. By understanding the nuances and techniques for solving various math problems, you can excel academically and gain confidence in your mathematical abilities.
Whether you're a student, educator, or lifelong learner, this guide has provided valuable insights and practical advice for solving math problems with ease and confidence. From understanding basic arithmetic to tackling advanced calculus problems, we've explored the essential techniques and strategies for success.
By embracing math problems and developing your problem-solving skills, you can achieve success in math and beyond, and make informed decisions in your personal and professional life. So, take on the challenge of math problems and discover the joy and satisfaction of solving them with creativity and confidence.